澳门正版资料免费资料大全
- 管家婆一码一肖资料大全水果
- 新澳门彩历史开奖记录大全
- 2024年澳门今晚开奖号码
- 澳门一码一肖一特一中
- 新澳门六开奖号码记录
- 澳门一肖一码100准免费资料
- 2024新奥历史开奖记录
- 澳门王中王100%的资料
- 2023澳门管家婆资料正版大全
- 打开澳门免费资料大全
- 澳门六开奖结果2023开奖记录
- 2024澳彩开奖记录查询表
- 管家婆一码一肖资料
- 2024澳门天天开好彩大全
- 2024年新澳彩开奖结果
- 管家婆一码一肖资料大全
- 2024澳门正版资料免费大全
- 2024港澳宝典正版资料下载
- 2023管家婆资料正版大全澳门
- 2024年新澳开奖结果
- 2023管家婆精准资料大全免费
- 2024新澳免费资料
- 2023澳门六今晚开奖结果出来
- 澳门六开奖结果2024开奖记录
- 新澳彩资料免费资料大全
- 2024年正版资料免费大全
- 2023澳门资料大全正版资料免费
- 澳门天天彩免费资料大全免费查询
- 2024澳门资料大全免费
- 新澳门彩历史开奖记录走势图
- 2024香港最新开奖结果查询
- 2024年最旺的四大生肖
- 2O24管家婆一码一肖资料
- 2o24管家婆一码一肖资料
- 2024新澳门天天开好彩大全
- 澳门六开奖结果2024开奖记录查询
- 今期澳门三肖三码开一码
- 2024澳门资料免费大全
- 新澳澳门免费资料网址是什么
- 澳门一肖一码100%精准一
- 2024澳门精准正版资料
- 新澳门资料大全正版资料2023
- 2023年澳门今晚开奖号码
- 2024香港历史开奖记录
- 2024年港彩开奖结果
- 7777788888王中王中王
- 7777788888精准管家婆凤凰网
- 2023澳门天天开好彩大全
- 2024澳门管家婆资料正版大全
- 最准一码一肖100%精准
- 管家婆一肖一码中100%命中
- 新澳2024年精准一肖一码
- 2024年白小姐开奖结果
- 新澳门最新开奖记录查询
- 49图库资料免费大全资料澳门
- 澳门最准一肖一码一码配套成龙A
- 澳门最准一肖一码一码配套成龙a
- 管家婆一肖一码最准
- 2024澳门资料大全正版资料
- 澳门最准一肖一码一码配套成龙W
- 澳门最准一肖一码一码配套成龙w
- 7777888888管家婆中特
- 新澳门今天开奖结果查询表
- 2024澳门历史记录查询
- 2024澳门六今晚开奖记录
- 新澳门历史开奖结果近期十五期
- 管家婆一码一肖100中奖
- 澳门特一肖一码免费提
- 管家婆2024免费资料使用方法
- 二四六香港管家婆期期准资料大全
- 六盒宝典2024年最新版
- 澳门天天彩正版免费全年资料
- 正版资料免费资料大全
- 澳门六开奖结果2023开奖记录查询网站
- 澳门开彩开奖结果历史
- 2024新澳门002期管家婆
- 2024澳门管家婆资料大全免费
- 最准一肖一码一一子中特
- 澳门六开奖结果2023开奖记录今晚
- 2024香港今晚开奖号码
- 管家婆一肖一码最准资料公开
- 管家婆必出一肖一码一中一特
- 2024新澳彩免费资料
- 新澳好彩免费资料查询
- 新澳彩资料免费长期公开
- 86949.cσm查询大赢家澳彩
- 2024年正版管家婆最新版本
- 2023年澳门天天彩开奖记录
- 澳门今晚必中一肖一码准确9995
- 2024新版生肖表图片
- 2024年香港6合资料大全查
- 新澳门免费资料大全
- 管家婆八肖版资料大全
- 2024澳门新资料大全免费
- 香港二四六开奖免费资料大全
- 新澳门全年资料内部公开
- 澳门管家婆一肖一码100精准
- 管家婆2023正版资料大全
- 2023资料免费大全
- 新澳门历史开奖结果近期十五号
- 新澳门资料大全正版资料2024年免费下载
- 2023澳门正版开奖结果
港彩高手出版精料
澳门精华区 香港精华区
【管家婆一句话】

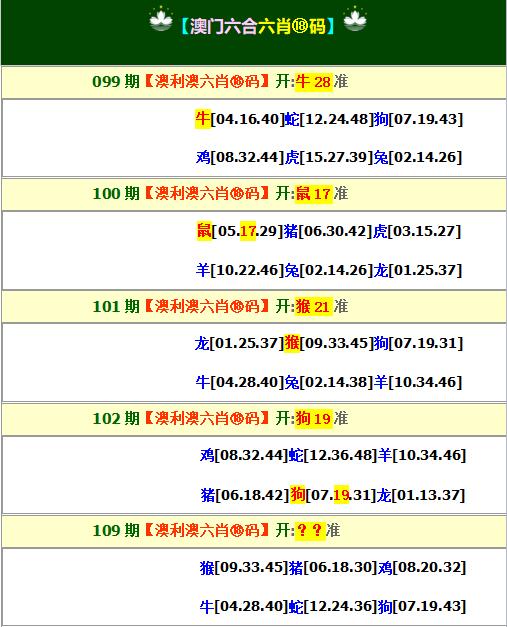
【六肖十八码】
澳门正版资料澳门正版图库
- 头条名词
- 水果爷爷
- 小龙女心经
- 118内幕资料
- 澳利澳九肖
- 澳门大三巴
- 茶话诗
- 通缉令-2
- 老综合资料A
- 救世报
- 澳门佬
- 澳门理财婆
- 澳门来料精华
- 老钱莊
- 澳门马票
- 澳门神庙
- 澳门生肖皇
- 跑狗图A
- 金牌谜语
- 雷锋四字真言
- 爆笑水果奶奶
- 玄机兔耳
- 孤狼猛料
- 中指猫神
- 小兔鸟
- 六合红字
- 金牛好彩
- 鸿运财神到
- 鸿运网
- 鸿运谜语
- 鸿运平特王
- 富贵旺码
- 猪八戒开奖A
- 猪八戒彩报
- 红灯笼A
- 赤兔解密
- 六合趋势图
- 大明谋臣
- 赤兔五肖
- 周公解梦贴
- 金牛大强运
- 宝宝四肖
- 正版小幽默
- 内幕信封
- 金牛密爆
- 中奖号码
- 必中四肖S
- 你的富爸爸
- 澳门金猪图
- 金牛两面高手
- 七肖无敌14码
- 七品茶
- 六合英雄传
- 四字彩报
- 自由人二肖六码
- 白小姐高级会员
- 天机不可泄露
- 三肖绝杀
- 新财神报
- 六合宝典红
- 金牛高手榜
- 封神计划
- 太极侠
- 118开奖高手
- 猪八戒平特一肖
- 雷锋精神
- 白小姐玄虎
- 白小姐心水
- 福兔财神
- 金牛秘报A
- 猪八戒彩报A
- 玄武周刊
- 牛派救世报
- 猜猜谜语特
- 曾道人信箱另版
- 另版澳门挂牌
- 澳门读者论坛
- 八卦神算
- 神算挖呀挖
- 一本万利
- 八仙神算
- 芳草地
- 金猴王
- 澳门铁算盘
- 澳门天机
- 木子辉歌
- 澳门黄金金龙
- 澳门单吊一肖
- 澳门钻石十五码
- 澳门风水平特
- 澳门六合风水
- 澳门一点通
- 澳门定乾坤
- 澳门飞龙宝典
- 澳门金手指
- 澳门乾坤宝典
- 澳门锦囊宝典
- 澳门白姐锦囊
- 澳门赌王天书
澳门正版资料人气超高好料
- 神奇八卦图
- 澳门四不像
- 新趣味幽默
- 澳门青龙报
- 澳门女财神
- 澳门女人味
- 每日闲情图
- 澳门码头诗
- 澳门猛虎报
- 澳门传真图
- 老版跑狗图
- 另版跑狗图
- 澳六合头条
- 澳门两肖特
- 四组三连肖
- 看图解特码
- 开心果先锋
- 金钱豹功夫
- 今日闲情1
- 今日闲情2
- 济公有真言
- 澳幽默猜测
- 皇道吉日图
- 澳门红虎图
- 鬼谷子爆肖
- 功夫早茶图
- 挂牌平特报
- 观音彩码报
- 新挂牌彩图
- 新管家婆图
- 凤凰天机图
- 佛祖禁肖图
- 赌王心水图
- 单双中特图
- 财神报料图
- 八仙指路图
- 八仙过海图
- 澳门不夜城
- 澳门跑马图
- 澳门七星图
- 二尾四码图
- 财神玄机报
- 内幕特肖A
- 12码中特图
- 七肖中特报
- 管家婆密传
- 东成西就图
- 新图库禁肖
- 三八婆密报
- 澳门挂牌
- 澳话中有意
- 一句真言图
- 澳门蛇蛋图
- 特码快递报
- 六合家宝A
- 波肖尾门报
- 生肖属性
- 白小姐会员
- 澳门孩童报
- 澳门牛头报
- 澳门大陆仔
- 澳门老人报
- 公式规律
- 凤凰卜封图
- 千手观音图
- 发财波局报
- 看图抓码图
- 神童透码报
- 高手解特
- 红姐内幕图
- 鱼跃龙门报
- 腾算策略报
- 内部传真报
- 六合英雄报
- 内部猛料
- 波肖一波中
- 36码中特图
- 30码中特图
- 曾道人暗语
- 澳门天线宝
- 梦儿数码报
- 澳门大陆报
- 通天报解码
- 凤姐30码图
- 澳门签牌图
- 内幕特肖B
- 天天好彩
- 值日生肖图
- 三怪禁肖图
- 博彩平特报
- 马会火烧图
- 无敌猪哥报
- 劲爆龙虎榜
- 白小姐救世
- 澳门男人味
- 六合简报图
- 周公玄机报
- 正版射牌图
- 澳门一样发
澳门正版资料免费资料大全
- 澳门抓码王
- 六合家宝B
- 高手预测
- 传真八点料
- 白小姐密报
- 一字解特码
- 文字资料
- 全年资料
- 金手指论坛
- 幽默玄机坛
- 管家婆论坛
- 小黄人幽默
- 四不像玄机
- 内幕传真图
- 金多宝传真
- 正版通天报
- 新生活幽默
- 狼女侠客图
- 平特一肖图
- 彩霸王六肖
- 庄家吃码图
- 福建打枪客
- 澳百万文字
- 顶级论坛网
- 好运一点通
- 如意论坛网
- 通天论坛网
- 天府论坛网
- 横财富论坛
- 八码论坛网
- 名人堂论坛
- 奥利奥论坛
- 澳门蓝月亮
- 济公救世坛
- 何仙姑论坛
- 小龙女论坛
- 澳门资料库
- 广西二五仔
- 六合财神
- 六合皇料
- 18点来料
- 天下精英
- 金明世家
- 马会官方
- 百万富翁
- 凤凰马经
- 各坛精料
- 特区天顺
- 博发世家
- 高手杀料
- 天线宝宝
- 蓝月亮料
- 十虎权威
- 彩坛至尊
- 传真内幕
- 王牌猛料
- 内部资料
- 澳门惠泽
- 任我发料
- 精选玄机
- 镇坛之宝
- 跑狗论坛
- 广西三八网
- 挂牌论坛
- 淘码论坛
- 四不像论坛
- 报彩神童论坛
- 老奇人论坛
- 港澳站
- 天线宝宝论坛
- 王中王论坛
- 澳彩资料网
- 夜明珠论坛
- 红虎论坛
- 曾道人论坛
- 满堂红论坛
- 红双喜论坛
- 破码网论坛
- 百晓生论坛
- 六合通论坛
- 六合皇论坛
- 抓码王论坛
- 创富网论坛
- 博彩网
- 东成西就坛
- 六合大亨论坛
- 青龙阁论坛
- 聚彩堂论坛
- 大赢家论坛
- 港澳天空彩票
- 资料研究院
- 金钥匙论坛
- 观音救世坛
- 博彩皇论坛
- 天天好彩
- 刘伯温论坛
- 宝马论坛
- 123论坛坛
- 88开奖论坛
澳门正版资料免费资料大全
- 2024年澳门今晚开奖号码
- 澳门一码一肖一特一中
- 澳门最精准正最精准龙门客栈
- 刘伯温精选四肖八码期期准
- 2024澳门正版资料大全免费
- 2024年买马生肖表
- 天天开奖澳门天天开奖历史记录
- 澳门一肖一码100精准2023
- 白小姐三肖三码必开一码开奖
- 澳门一肖一码100%准确
- 香港历史最快开奖结果
- 正版49图库
- 2023澳门正版资料全年免费
- 管家婆精准资料大全免费
- 管家婆三期必中一期的人物
- 2024年澳彩综合资料大全
- 2023年香港港六资料查询
- 澳门最精准正最精准龙门
- 2023年正版资料免费大全
- 正版资料与内部资料
- 626969澳门精准资料2021期
- 澳门管家婆免费资料的特点
- 2023年香港资料精准
- 2023澳门今晚中必一肖一中特
- 平码中一个号怎么算
- 最准一肖一码100%中奖中
- 新澳2023管家婆资料
- 六给彩开奖结果纪录
- 澳门一肖一码100精准
- 管家婆一肖一码澳门码资料
- 澳门一肖一码必中一肖今晚mba
- 最准一肖一码100%最准最新版
- 澳门免费资料大全精准版
- 澳门精准一肖一码一码配套成龙
- 下载澳门资料大全
- 新澳门精准一肖一码准确公开
- 管家婆正版今晚开奖结果
- 新澳门历史记录查询最近十期
- 2023澳门新资料大全免费
- 澳门一肖一码资料
- 管家婆三期开一期精准的背景
- 管家婆免费2023资料大全
- 香港王中王最快开奖结果
- 管家婆一肖一码资料大全
- 42982金牛网论坛
- 澳门四肖八码期期准中特更新
- 管家婆一肖一马最早出图
- 管家婆精准资料大全
- 2024新澳彩资料免费资料大全
- 澳门码鞋一肖一码
- 澳门一码中精准一码免费中特论坛
- 管家婆三期开一期精准是什么
- 管家婆2023资料精准大全
- 123澳门正版免费资料
- 2023澳门六今晚开奖结果出来85期
- 2023澳门六今晚开奖记录
- 澳门三肖三码精准100%王中王
- 香港最准最快的资料免费
- 澳门金牛版正版资料大全免费
- 澳彩资料免费资料大全的特点
- 2023澳门正版资料
- 澳门资料大全正版资料下载
- 2023澳门资料正版大全
- 2023澳门正版资料大全免费图片
- 2023一码一肖100%精准
- 7777788888管家婆中特
- 澳门三肖三码精准100%
- 澳门今晚必中一肖一码今晚澳门
- 澳门天天彩资料正版免费特色
- 新澳门2023历史开奖记录查询表
- 新澳门彩最新开奖记录查询表下载
- 新澳门资料大全正版资料2024年免费
- 管家婆2023正版资料
- 2024年12生肖49码图
- 香港码今晚开奖结果查询
- 香港管家婆资料正版公开
- 澳门一肖一码必中一肖期期精准
- 天下彩(9944cc)天下彩图文资料
- 香港最近15期开奖号码
- 澳门今晚开奖结果号码
- 澳门免费公开资料大全
- 2024最新12生肖号码
- 2024年香港今晚开奖结果查询
- 2023澳门今晚开奖结果是什么
- 2023年管家婆精准一肖
- 新澳门最新开奖结果记录历史
- 澳门资料大全免费资料
- 澳门管家婆一肖一码一中一开
- 管家婆2024全年免费资料
- 下载澳门六下彩资料官方网站
- 澳门最快最准资料免费手机网站
- 澳门一码中精准一码免费中特
- 2024新澳门姿料
- 一码一肖100准吗
- 2023年12生肖49码图
- 今天澳门一肖一码
- 二四六天下彩天天免费大全
- 新澳门正版资料
- 今期开奖结果今晚开奖结果
- 澳门最精准免费全网资料
- 管家婆免费资料三期必中
- 2023全年澳门资料免费看
- 2023澳门精准正版资料大全
- 本港台现场直播开奖报码开奖结果
- 晚上澳门开什么
- 四不像四不像
- 2023今晚澳门码开奖号码
- 澳门近期的历史记录
- 管家婆期期精准选一肖2021
- 新澳门六开最新资料查询
- 49图库免费的资料港澳
- 管家婆今期免费资料大全
- 2023澳门全年资料免费大全
- 2023澳门精准正版资料
- 2023新澳门资料免费大全
- 管家婆最准一码一肖
- 澳门金牛版资料免费大全
- 新澳彩开奖结果2023开奖记录查询
- 管家婆2023年正版资料
- 澳门正版资料大全免费看
- 澳门资料大全正版资料查询202
- 2023澳门正版免费资料
- 香港2023正版全年资料免费看
- 精准三肖三期内必中的内容
- 二四六(944cc)资料免费
- 2023年天天彩澳门天天彩
- 今晚精准一肖一码
- 246天天彩944CC二四六天天彩
- 天下彩(9944CC)图文资讯
- 新一码一肖100准正版资料
- 澳门正版资料大全
- 澳门一肖一码期期准中选料lk
- 660678王中王免费提供护栏六玄网
- 澳门今期开奖结果开奖查询
- 澳门正版资料免费大全新闻
- 澳门资料大全正版资料2023年
- 2023年香港港六开奖结果今天
- 2023澳门全年资料大全免费
- 黄大仙一肖一码开奖37b
- 香港最快开奖现场直播资料
- 澳门2023正版资料大全完整版
- 2023澳门今晚开什么号码
- 2023澳门彩免费资料大全
- 2023澳门六今晚开奖直播回放
- 免费香港资料大全
- 香港今期开奖结果号码
- 白小姐三肖三期必出开奖
- 王中王中特网资料大全
- 2023澳门今晚一肖一码
- 澳门6合开彩开奖结果
- 一码一肖100准资料应用
- 澳门金牛版42260Cm
- 澳门4949彩论坛高手
- 旺角彩二四六天空彩赢彩
- 精准澳门平特一肖
- 2023澳门正版资料免费图
- 澳门精准免费资料大全聚侠网
- 香港2023精准资料
- 2023年正版管家婆最新版本
- 管家婆资料精准大全
- 2023澳门资料免费大全
- 白小姐精选四肖必中一肖
- 2023香港历史开奖记录
- 管家婆三期必开一期2023
- 澳门四肖八码期期准精选资料一页
- 王中王一肖一特一中
- 二四六天天好(944CC)246天彩
- 二四六天天好(944cc)246天彩
- 澳门最准一码100%
- 澳门一码一肖100准王中
- 一码一肖一特
- 香港一肖一码100准确
- 今天澳门晚上出什么马
- 2022澳门正版资料全年免费公开
- 精准三肖三期内必中是什么
- 2023澳门资料大全免费彩色
- 2023澳门今晚开奖结果56期
- 一肖一码中持一一肖一子
- 管家婆正版图片大全
- 493333王中王开奖结果 127.0.0.1
- 澳门最快最精准资料大全
- 正版管家婆
- 2023年一码一肖100精准
- 二四六天好彩(944cc)246天天
- 澳门正版资料免费阅读
- 澳门管家婆四肖选一肖期期准
- 澳门资料大全正版资料查询2022年
- 新澳彩开奖结果历史记录表格查询
- 2023澳门今晚开什么
- 澳门王中王免费资料独家猛料
- 2024澳门历史开奖记录
- 四肖八码期期准精选
- 澳门一肖一码100精准澳门
- 2023年一码一肖100%准确
- 2023澳门精准正版澳门码
- 4777777现场直播开奖记录678
- 六盒宝典2021年最新版
- 澳门天天彩正版免费资料大全
- 4949澳门免费资料大全笔记本
- 澳门直播开奖现场下载
- 2022年澳门正版资料免费公开
- 香港本期开奖结果今晚
- 澳门金牛版网站论坛
- 澳门正版资料免费大全新闻最新大神
- 管家婆软件免费版
- 澳门彩开奖结果开奖记录表最新
- 香港正版资料大全
- 今晚新澳门必中一肖一码
- 2022全年资料免费大全下载
- 626969澳彩资料大全2020期 - 百度
- 王中王资料精选
- 澳门六开全部免费资料2021
- 二四六天天好(944cc)46天彩
- 2023一肖一码必中一肖
- 管家婆精准资料大全功能
- 2021澳门资料大全正版资料
- 2021澳门最快最准开奖结果
- 2020年香港今晚开奖结果
- 一肖一码100%中奖
- 澳门4949开奖现场直播下载
- 管家婆期期准免费资料
- 2023澳门三肖三码100%
- 2023一肖一码100%准确
- 新澳门正版资料免费更新1181
- 香港资料大全 正版资料
- 澳2023一码一肖100准确
- 澳网最新比赛结果
- 澳门最快开奖号码
- 澳门资料大全正版资料2
- 626969cc澳门资料大全2021年336
- 澳门彩今晚开码结果记录
- 澳门一肖一码澳门
- 555525oom王中王金牛版
- 一肖一码100准中奖澳门
- 香港内部马料
- 2021年澳门资料免费大全
- 管家婆期期准精选资料大全
- 期期四肖选一肖
- 2021全年资料免费大全
- 开奖结果蓝月亮精选枓
- 2021年澳门正版免费资料全解
- 2021年澳门今晚开奖结果
- 香港开马开奖现场直播
- 白小姐四选一肖期期准
- 2021年澳门正版免费资料
- 王中王中马












